Finding Patterns in Chaos
Lesson 11
As we conclude our explorations of the connections between mind, number
and reasoning we return once again to pattern in nature and number and
the way in which mind seeks for such correspondences. Sometimes it is useful
to realize the ground out of which our propensity for counting, measuring
and ordering things around us springs. The human mind for example springs
from our efforts to answer the question what comes next. The infant crying
for food and getting breast or bottle learns very quickly what comes next
if you're hungry and cry. And while there are exceptions and complications
( sometimes when you're hungry, you get your diaper changed,) she learns
to follow a rule that says something like
If hungry
then cry
if cry
then food.
Can you think of similar "rules" infants seem to work out? Try stating
the rules using the "if - then" format illustrated in the hungry
baby example.
If X
then Y
If Y
then Z
Admittedly, other animals seem to use similar strategies and get similar
results, but only humans seem to very quickly progress to a stage where
a more sophisticated question about what come next emerges. It probably
begins with how long do I have to cry before I get what I want, but by
the time most children are two years old they can do what a young acquaintance
of mine did recently. Driving with her parents past a very large statue
of a very friendly looking polar bear outside a very large automobile dealer's
retail sales yard, which her parents called to her attention with the usual
"Look at the big polar bear. Isn't it cute?", Mali responded with one of
her very first English sentences. "Can we buy it?" she said. Here is a
child who has not only figured out what comes next, but a god deal about
her culture and even more about what it is humans are trying to do by knowing
or guessing what comes next. Mali is into controlling what happens to her,
and so are we all. Mali's rule now seems to have many levels.
If I want X,
If I don't have X,
If mommy and daddy don't have X,
If somebody else has X,
Then mommy and daddy can buy X.
If mommy and daddy know I want X,
If I ask them for X,
If they can buy X,
Then they will get X for me.
In fact, Mali probably even has some rules like "I know sometimes they
don't buy X, Y Or Z for me ,but sometimes they do." She's probably even
on her way to a rule that goes something like
If You ask and it doesn't hurt,
Then You never can tell.
We've already done a good deal of this sort of if-then talking and thinking
about making predictions and guesses to win bets (like winning the lottery)
and/or decide what we ought to do under certain circumstances like driving
with a storm threatening. In those cases we've spent sometime developing
rules for making the best decision and/or best bet. What has enabled us
to do that is that we've come up with ways of counting the possible outcomes,
estimating the likelihood of obtaining the outcome we want, deciding what
chance we are willing to take or what losses we can accept, and acting
accordingly. In some of those instances we've had to remind ourselves that
while we have an idea of how likely certain outcomes are, we really don't
know what will come next. If the weather forecasters tell us there is a
50% chance of rain or snow we are, in fact equally sure that it will or
won't rain or snow. We've learned to live without being able to predict
exactly, while trying to make the best decisions possible in the face of
uncertainty. Most of the really important problems facing us individually
and collectively are exactly this kind of problem, problems that are so
complex we can't achieve certainty by controlling all the factors affecting
the outcomes we're concerned with.
Predicting the weather is exactly such a problem. What weather
forecasters are trying to do is to predict the unpredictable, guess well
about a our
world weather system, a system so complex that any attempt to say
exactly what will happen next is almost impossible.
How can human beings who want to know what to do next live with that
kind of uncertainty? Why it seems like we're living in chaos.
To which the mathematician answers, "I wonder what chaos is like? I
mean how does chaos look? How does the weather look? Do we have any
models for Chaos? How can we make models for the weather?"
Here is a short description of the theory of complex systems, Chaos Theory, from a world wide web site of
the Eastview Math Department designed by Andrew McHardy and written by
Sara Styles and Alex Lee of Eastview Secondary School in Barrie, Ontario,
Canada. What Sara and Alex say applies to weather as well as hearts,
faucets and markets.
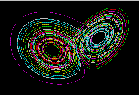 In fact, chaos theory developed
form the work of Edward Lorenz, a meterologist who, while attempting model
air convection, discovered a distribution that later came to be called
a strange attractor. His model had three parameters, yet this simple system
proved that consistently accurate weather prediction is beyond human grasp.
His explanation of what he found included a notion that has become one
of the most famous explanations of chaos theory applications in weather
predicting. The notion is that one stroke of a butterfly's wing in Central
America could produce a typhoon in Hong Kong at some future point. What
you see pictured is the distribution that Lorenz discovered. The fact that
it looks like a butterfly's wings has nothing to do with Lorenz's notion,
except that minds like yours and mine are always struck by the appearance
of such striking coincidences of pattern in what seems to be accident.
That is in fact what makes chaos theory so interesting. The pattern is
also sometime's called the owl's mask, and may be what Loren Eisley notes
Thomas Hardy says is "but one mask of many worn by the Great Face behind.
"
In fact, chaos theory developed
form the work of Edward Lorenz, a meterologist who, while attempting model
air convection, discovered a distribution that later came to be called
a strange attractor. His model had three parameters, yet this simple system
proved that consistently accurate weather prediction is beyond human grasp.
His explanation of what he found included a notion that has become one
of the most famous explanations of chaos theory applications in weather
predicting. The notion is that one stroke of a butterfly's wing in Central
America could produce a typhoon in Hong Kong at some future point. What
you see pictured is the distribution that Lorenz discovered. The fact that
it looks like a butterfly's wings has nothing to do with Lorenz's notion,
except that minds like yours and mine are always struck by the appearance
of such striking coincidences of pattern in what seems to be accident.
That is in fact what makes chaos theory so interesting. The pattern is
also sometime's called the owl's mask, and may be what Loren Eisley notes
Thomas Hardy says is "but one mask of many worn by the Great Face behind.
"
The system that is the earth's atmosphere is not only complex, it is a
system that is characterized by sensitive dependence, that is very small
changes in the system produce very large effects. Later in this course
you'll work on some material that deals with that notion mathematically,
but for the moment I 'm interested in trying to give you to think about
sensitive dependence in your own experience. What happens, for example, if
you make a small error orienting yourself using a map and a compass.
Suppose you are off 1 degree to the east in trying to walk one mile north,
how far off target would you be. Do you know how to calculate this answer.
If you do, calculate how many feet off target you would be. If not, or to
check your answer, look at the way
trigonometry can be used to solve such a problem.
Incidentally, sensitive dependence on initial errors in compass reading
can be, and are dealt with by those who know the way of the compass and
the ways of the woods. I learned that lesson from a neighbor, when for
a time, I lived on forty acres in a national forest.
Imagine that you're a city dweller, living for the first time in the
woods and concerned that an old Finnish logger who has a permit to cut
pulp next to your land is cutting trees on your land. Imagine that you
work up your courage and say, "Hugo, I think you're cutting trees on my
land."
And he says, "Thomas, I don't think so., but let's go look."
We walk into the middle of what I've come to think of as my woods, and
the black spruce are lying all around us and work our way over and around
the downed trees to the southern edge of the cut, my edge.
Hugo says, "See Thomas, this is where we're stopping. If you walk a
east west compass line from here,
you'll come on the old corner post that marks the edge of your forty."
I know the post, I'd found it and knew it marked the corner he said
it did. I say, "I'll do that Hugo," and turn to walk the line, taking out
my compass.
And he says "Oh, by the way Thomas, have you ever tried to walk a line
in the woods."
I turn back to him and he says "It'll work best if you site your compass
at a spot, like that big tree there and walk to it, and then aim at another,
and walk to it. You know, its really hard to walk a straight line with
all the trees in the way."
I thank him, follow his advice, come out of the thick woods and into
his old tracks, at the edge of an opening and walked in his tracks, following
my compass line, to my corner post. I learn a good many things about moving
in the woods and about being a good neighbor from my Finn pulp cutter.
Not the least of them was that one of the models we use in making predictions
and conclusions applies to walking in the woods.
What Hugo knew from experience was, if you take many measures of the
direction you want to go in, the errors you make in any one measure, will
be balanced and canceled by the random errors you make in the other observations.
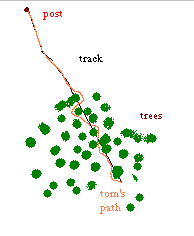 Statisticians refer
to this fortunate tendency of errors to cancel each other out when they
measure the standard error of a series of measures. Hugo was woods statistician.
Most of us have used similar ways of making sure we get our errors to balance
each other. This is especially easy when our problem is of the kind we
just considered, a problem that involves a simple linear model. We just
want to be sure we're moving in the right direction. In fact we can represent
the problem and the Hugo's solution nicely using a linear model. We just
want to be sure we're moving in the right direction. In fact we can represent
the problem and the Hugo's solution nicely using a linear model. You can
see Hugo's technique illustrated in the crude sketch to our left. The path
through the trees necessarily takes our walker to either side of a course
that would be a straight line to his objective. In fact the straight line
is an idealized version, a linear model of the true path the walker follows.
The history of physics, chemistry and biology involves the search for such
models.
Statisticians refer
to this fortunate tendency of errors to cancel each other out when they
measure the standard error of a series of measures. Hugo was woods statistician.
Most of us have used similar ways of making sure we get our errors to balance
each other. This is especially easy when our problem is of the kind we
just considered, a problem that involves a simple linear model. We just
want to be sure we're moving in the right direction. In fact we can represent
the problem and the Hugo's solution nicely using a linear model. We just
want to be sure we're moving in the right direction. In fact we can represent
the problem and the Hugo's solution nicely using a linear model. You can
see Hugo's technique illustrated in the crude sketch to our left. The path
through the trees necessarily takes our walker to either side of a course
that would be a straight line to his objective. In fact the straight line
is an idealized version, a linear model of the true path the walker follows.
The history of physics, chemistry and biology involves the search for such
models.
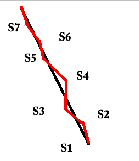
Let's take our model making one step further and look at this schematic
model for following Hugo's directions. The jagged line represents the true
path of our walker, and it swings from side to side of the model path each
time the walker take a compass siting at points S1, S2, and so on. As our
compass user gains experience and takes mor frequent compass readings,
the deviations from the true path become smaller. But no matter how long
the user practiced, or how frequently she checked her compass bearings,
there would still be small errors and small corrections. Unless, of course,
some other systematic factor was pushing our walker off the true path,
like a difference between true north and magnetic north, or a steady west
wind blowing a boat being steered by compass east of true north. These
factors would take one off the true path and experienced compass users
adjust their readings to account for such systematic sources of error.
Each time scientists try to build linear models for real world phenomena
a similar process produces a similar search for a true path model. In fact
observation of real paths followed by animals and aboriginal peoples has
produced a curvilinear model for the way people and animals follow straight
line paths. It's called a sine wave and is produced by plotting
the trigonometric function we used to solve our problem about how far off
we'd be, if we made a 1 degree error in our first compass siting. What
mathematics dose is give us models for idealized representations of what
really happens. Sometimes those models apply directly to the way we behave
and we can then say that when human beings try to walk a straight line
between point A and point B, their true path would approximate the following
shape.

This pattern characterizes as an ideal form the behavior of a great
many natural phenomena ranging form brain waves to ocean waves. It is the
kind of model for such phenomena that linear mathematics generates. But
some phenomena, like the weather are too complex for such simple models
to work in characterizing them. Which brings us around again to chaos theory.
Perhaps you can get the best idea of how chaos theory builds its models
by visiting a site that is devoted to introducing us to chaos
visually <http://johnbanks.maths.latrobe.edu.au/chaos/animated/index.html>.
Work your way through Dr. Banks site beginning with The
Idea of a System page, following the sequential
order of the pages as the site suggests. Once you've look through
these materials enough to feel yo have an idea about how the theory works,
you can continue your explorations of minds efforts to model chaos.
For your second trip through chaos we're interested in your exploring
a variety of world wide web sites that deal with chaos theory to see the
way in which mathematical models come into play in our efforts to understand
the world around us . This time instead of trying to direct you towards
specific outcomes, we want to ask you to explore, imagine, think about
the ways in which building idealized models helps to understand and solve
real problems, and help us to find the patterns that bring order to what
appear to be random events. While such patterns don't enable us to make
precise predictions, they at once help us to tolerate and appreciate uncertainty,
and to make more informed decisions about what to do in the face of uncertainty.
Then we'll ask you to write a 600 word reaction that summarizes what you
found searching the web sites, explains how what you found use models to
understand complexity, and relates what you found to the explanation of
chaos theory that you found at Dr. Banks site.
Here are a dozen sites that you might start with, and you will be able
to find more by following links from these pages to other sites. In doing
your chaos project, you should only try to deal with three or four sites
that you see as being related and of interest to you. But you will want
to visit a good many sites before you select those you want to write about.
Start by taking a brief look at all of these sites and then go back to
those that interest you.
{This list is a sample and we will need to pick the sites for
this list with care to insure both a wide variety of topics and fast loading
sites.}
http://www.astrologer.com/chaology/earth.html
http://www.intelligraphics.com/per/derrelb.html
http://www.hu.ic.ac.uk/scicom/chaos.htm
http://www.cs.hmc.edu/~kevin/chaos/chaos.html
http://tqd.advanced.org/3493/noframes/main.html
http://www.netins.net/showcase/ddtm/main/chaos.html
http://www.trajecta.com/white.htm
http://millbrook.lib.rmit.edu.au/fractals/exploring.html
http://trixie.eecs.berkeley.edu/~wrdavis/chaos/chaos.html
http://www.worldweb.com/AHFMR/janfeb96/Chaos.html
http://astro.temple.edu/~callahan/hjs/framed/rice.html
http://www.prairienet.org/business/ptech/txt/chaostry.html
Possible alternative exercise. {Read an excerpt from The
Left Hand of Darkness that explores the utility of uncertainty.}
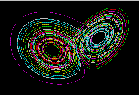 In fact, chaos theory developed
form the work of Edward Lorenz, a meterologist who, while attempting model
air convection, discovered a distribution that later came to be called
a strange attractor. His model had three parameters, yet this simple system
proved that consistently accurate weather prediction is beyond human grasp.
His explanation of what he found included a notion that has become one
of the most famous explanations of chaos theory applications in weather
predicting. The notion is that one stroke of a butterfly's wing in Central
America could produce a typhoon in Hong Kong at some future point. What
you see pictured is the distribution that Lorenz discovered. The fact that
it looks like a butterfly's wings has nothing to do with Lorenz's notion,
except that minds like yours and mine are always struck by the appearance
of such striking coincidences of pattern in what seems to be accident.
That is in fact what makes chaos theory so interesting. The pattern is
also sometime's called the owl's mask, and may be what Loren Eisley notes
Thomas Hardy says is "but one mask of many worn by the Great Face behind.
"
In fact, chaos theory developed
form the work of Edward Lorenz, a meterologist who, while attempting model
air convection, discovered a distribution that later came to be called
a strange attractor. His model had three parameters, yet this simple system
proved that consistently accurate weather prediction is beyond human grasp.
His explanation of what he found included a notion that has become one
of the most famous explanations of chaos theory applications in weather
predicting. The notion is that one stroke of a butterfly's wing in Central
America could produce a typhoon in Hong Kong at some future point. What
you see pictured is the distribution that Lorenz discovered. The fact that
it looks like a butterfly's wings has nothing to do with Lorenz's notion,
except that minds like yours and mine are always struck by the appearance
of such striking coincidences of pattern in what seems to be accident.
That is in fact what makes chaos theory so interesting. The pattern is
also sometime's called the owl's mask, and may be what Loren Eisley notes
Thomas Hardy says is "but one mask of many worn by the Great Face behind.
"
 Statisticians refer
to this fortunate tendency of errors to cancel each other out when they
measure the standard error of a series of measures. Hugo was woods statistician.
Most of us have used similar ways of making sure we get our errors to balance
each other. This is especially easy when our problem is of the kind we
just considered, a problem that involves a simple linear model. We just
want to be sure we're moving in the right direction. In fact we can represent
the problem and the Hugo's solution nicely using a linear model. We just
want to be sure we're moving in the right direction. In fact we can represent
the problem and the Hugo's solution nicely using a linear model. You can
see Hugo's technique illustrated in the crude sketch to our left. The path
through the trees necessarily takes our walker to either side of a course
that would be a straight line to his objective. In fact the straight line
is an idealized version, a linear model of the true path the walker follows.
The history of physics, chemistry and biology involves the search for such
models.
Statisticians refer
to this fortunate tendency of errors to cancel each other out when they
measure the standard error of a series of measures. Hugo was woods statistician.
Most of us have used similar ways of making sure we get our errors to balance
each other. This is especially easy when our problem is of the kind we
just considered, a problem that involves a simple linear model. We just
want to be sure we're moving in the right direction. In fact we can represent
the problem and the Hugo's solution nicely using a linear model. We just
want to be sure we're moving in the right direction. In fact we can represent
the problem and the Hugo's solution nicely using a linear model. You can
see Hugo's technique illustrated in the crude sketch to our left. The path
through the trees necessarily takes our walker to either side of a course
that would be a straight line to his objective. In fact the straight line
is an idealized version, a linear model of the true path the walker follows.
The history of physics, chemistry and biology involves the search for such
models.
