Trigonometry
One of the most useful applications of linear models, trigonometry, gives
us very accurate predictions about how far astray we wander if we make an
error of a specified size. It uses one of the oldest and most fundamental
of all mathematical theorems, the Pythagorean theorem. ( If you're
interested in learning more about Pythagoras and his theorem you could
view a video from Bronowski's series The Ascent of Man series,
titled "Man the Measure of All Things")
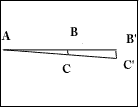
Essentially, if we imagine our compass user trying to go straight east
from point A to Point B and being off 1 degree south, the attached drawing
suggests what happens. If the distance traveled is 1000 meters, the
distance from B to C can be obtained by using the fact that the angle A is
known and therefore the length of BC can be calculated. We proceed by
looking up the sine ( which is the value obtained by dividing the side
opposite the angle by the hypotenuse in the right triangle formed of an
angle of 1 degree with hypotenuse AC of 1000 meters) in a table of
trigonometric functions. The value is .01745. If I then multiply that
value by the distance traveled (1000 meters) I know the traveler is 17.45
meters south of his target. If he proceeds another 1000 meters to C', how
far south of his target will he be?

