Phys 3041 Notes
©1997 Jonathan Maps. These notes may not be redistributed or duplicated in any form, print or electronic, without permission. Permission is granted to establish electronic hypertext links to these original documents only.
Return to the previous topic, electric potential.
One way to classify materials electrically is in terms of the ease with which charges can move through the material. In the case of solid materials, the chief consideration is the behavior of the electrons associated with each atom. In some solids practically all the electrons are bound to an atom and are immobile. Such materials are electrical insulators. In contrast, in metals each atom can contribute one or more electrons to a shared pool of highly mobile charges called the conduction electrons. These electrons are relatively free to move throughout the sample in response to an applied electric field (or associated electric potential). Such materials respond to an applied voltage with a continuous flow of charge. The rate at which the charge flows constitutes the electric current. Consider a piece of metal wire containing some mobile charges.
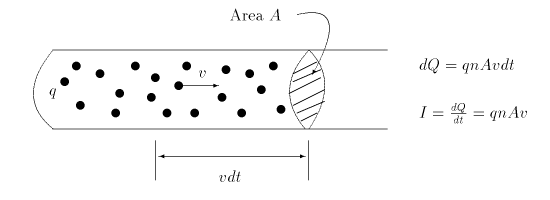
Let's make some simplifying assumptions for the moment. The particles constituting the electric current all carry a charge q and all move at the same speed v down the wire in response to an applied voltage. (In the case of electrons, the charge q = -e.) The cross-sectional area of the wire is A and the number of charges in a unit volume is n, usually called the number density. During a short time interval, some of the particles in the wire will reach the surface shown and pass through. During a time interval dt only those particles that are close enough -- within v dt of the surface -- will reach it. Particles starting farther to the left won't pass through the surface until later. So all the particles within a volume of Av dt pass through the marked surface during the time dt. The total number of such charges is just n Av dt, and since each particle carries a charge q, the total amount of charge that passes through the surface during dt is just dQ = nqAv dt. The electric current is just the rate at which charge passes this surface, I=dQ/dt=nqAv. Electric current measures the rate at which charge passes a point in a circuit. Electric current generally flows in response to an applied electric field or applied voltage difference (recall that electric fields imply voltage differences: Ez = -dV/dz).
In the gravitational analog, the analog to electric current will be the rate at which "gravitational charge" passes some point on the slope (or reaches the bottom). In that case, the "current" is simply the rate at which mass passes down the slope, which can be found by counting the number of skiers that go down the hill in some selected time interval (and keeping track of the mass of each skier if they are not identical, as we assumed in the case of electrical charges).
A simple model can justify the approximation that the charged particles move at some average speed, and this model gives rise to the idea of electrical resistance. In moving through the metal, the conduction electrons -- our charged particles -- must negotiate the complex lattice structure of atoms that forms the wire. The atoms are vibrating due to thermal energy and the wire is populated by defects and impurities that pose obstacles to the electrons. As a result, the electrons are repeatedly scattered as they pass through the wire. We assume that each electron experiences a series of collisions separated by a time T. Let's also assume that these collisions, on average, leave the electron at rest immediately after, so that the electron gives up all its kinetic energy to the lattice of atoms. Between collisons, the charges are accelerated by the applied electric field and gain momentum. So during the time T between collisions the charges gain an average momentum mv=qET (recall that dp/dt=F, from Newton's 2nd law).
The charged particles also lose this much momentum, on average, at each collision every T seconds, so that the collision process can be modelled as an average drag force:
Fdrag = dp/dt = -qET / T = -qE
which balances, on average, the accelerating force provided by the electric field. As a result the electrons move, again on average, at a constant drift velocity v=qET/m. For electrons, the charge, q, has a magnitude of e and m is the electronic mass. Under typical
conditions for metals drift velocities are on the order of mm/s. The electric current can now be written in terms of the collison time T by re-writing v:
I= dQ/dt = nqAv = nqA (qET/m)
I = (nq2T/m)AE.
This result is Ohm's Law, somewhat disguised from its usual form in the context of electric circuits. The quantity nq2T/m is called the electrical conductivity of the material. The conductivity is large if T is large, that is if the collisions that slow the electrons occur infrequently. This leads to a larger current for the same applied electric field, E. The usual form of Ohm's Law can be obtained by considering the wire to have a length L. Multiplying the previous expression by L/L and grouping things appropriately gives:
I = (nq2T/m)A/L (EL)
The product EL is just the voltage difference, V, between the two ends of the wire. The other factor, (nq2T/m)A/L is called the conductance of the wire. The inverse of this is the more familiar resistance R = (m/nq2T)L/A. Note that the resistance is proportional to the length and inversely proportional to the cross-sectional area of the wire. The proportionality factor (m/nq2T) is called the resistivity of the material, just the reciprocal of conductivity. This leaves us with:
I = V/R or equivalently, V = IR.
In the gravitational analog, resistance can be mimicked by populating the ski slope with trees - "scattering" sites for the skiers. Each time a skier collides with a tree, he or she must pick themselves up and start out downhill from rest again. The more closely spaced the trees, the more frequent the collisions and the shorter the collision time T.

With a dense tree structure the "current" of skiers arriving at the bottom will be small, since their average speed acquired between collisions will be very small due to the high frequency of collisions, and the ski slope will have a high resistance. Also note that at the bottom of the hill the skiers will have very little kinetic energy. They have converted most of the initial potential energy available at the top into other forms (heat, sound in loud screams of agony) during the inelastic collisions with the trees. The initial energy has been dissipated - i.e. converted to forms other than the kinetic or gravitational potential energy of the skiers. The same is true in the electrical case. The initial electrical potential energy is converted into other forms as the electrons make their way through the wire, chiefly as thermal energy of the atomic lattice, as evidenced by increases in temperature -- in the case of a light bulb, a large enough increase to lead to the radiation of energy away as visible light.
When charge flows through a resistor, the initial potential energy is converted into thermal energy. During a short time interval dt, an amount of charge
dQ passes through the resistor. The potential energy lost by this bit of charge is VdQ, where V is the voltage difference between the two ends of the resistor. The rate at which this potential energy is converted to thermal energy is called the power dissipated by the resistor:
P = dU/dt = VdQ/dt = VI. Using Ohm's law, this can also be written as
P = I2R = V2/R.
Energy converted into heat this way is referred to as Ohmic or Joule heating.
Continue on to the next topic, DC circuits.

