
Reasoning With Mathematics
Lesson 10 - Making Bets and Decisions: The Gambling in Statistics
As we go on exploring the ways we manage the risks of being human, of engaging in species
specific behavior, we can use what we've come to understand about the rules of the games we
play to illuminate the way we make decisions about everything from drilling for oil and how to
invest in the stock market to evaluating the effectiveness of medical treatments and the
possibilities of there being of life elsewhere in the universe. We'll start by shooting some Craps.
. What we're interested in is applying Thomas Bayes <http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Bayes.html>,
"method by which we might judge concerning the probability that an event has to happen, in
given circumstances, upon supposition that we know nothing concerning it but that, under the
same circumstances, it has happened a certain number of times, and failed a certain other
number of times," by making some bets. Consider the following two situations:
Scenario One
Shirley's rich uncle Tom gives her airfare, Hotel accommodations in Vegas and $500 mad money.
Scenario Two
Shirley moved to Vegas. She's got money for rent and food for the next month and will get her
first paycheck in three weeks. Her baby needs a new pair of shoes.
Shirley decides to play craps in each of these situations. Think about how she should bet in each situation, bet, and roll the dice for up to five passes (until you either win or lose a turn) for each situation. If you lose all your money before you roll five passes, you are finished. Before you try playing lets review the rules of the game outlined on the Crapper' Delight Basics of Craps <http://home.earthlink.net/~compr/Basics.html> site again.
{call this up with button from separate file}
*********************************************************************************************************************
Understanding The Basics:
The casino game of Craps is played with a set of two perfectly balanced dice with each
die having six white dots numbered 1 through 6. The game is played by tossing the dice from one
of the short ends of the table to the other, making sure that both dice hit the opposite side wall of
the table; payoffs are made based on the number combination displayed when the dice come to
rest. The inside walls of the table are covered with a kind of serrated egg-carton foam, designed
to make the dice bounce around to assure randomness. Each throw of the dice is called a "roll".
Players take turn rolling the dice, clockwise around the table, and the player rolling at any given
time is called the "shooter". When a new shooter is given the dice, his or her first roll is called the
"come out" roll. This begins a new series of rolls by that shooter and lasts for as long as that
shooter continues to make winning rolls.
A new game in Craps begins with the come out roll. A "Come out" roll can be made only
when the previous shooter fails to make a winning roll -- more correctly known as "not making the
point", or "seven out". A new game then begins with a new shooter. If the current shooter does
make his point, the dice are returned to him and he then begins the new come out roll. This is a
continuation of that shooter's roll, although, technically, the come out roll identifies a new game
about to begin.
When the shooter fails to make his or her point, the dice are then offered to the next
player for a new come out roll and the game continues in the same manner. The new shooter will
be the person directly next to the left of the previous shooter.
On the come out roll, the pass line bet wins if the shooter rolls a 7 or an 11. The bet
loses automatically if the shooter rolls 2, 3 or 12. This is known as "rolling craps". If the shooter
rolls either 4 5 6 8 9 or 10, winning your bet now depends on whether the shooter will roll this
same number again before rolling any 7. Rolling any of these numbers on the come out roll is
called "establishing the point". Any number so rolled is thereafter referred to as the "point".
Establishing a point is an event that happens as the immediate result of the come out roll, unless
that come out roll results in 7, 11, 2, 3 or 12, in which case more rolls must be made until a point
is established.
It now becomes important to mention a device that looks like a hockey puck, called "the
puck". It is white on one side and black on the other, and is used by the dealers to identify the
point. Once the point is established by the shooter, the dealer will move this puck to that point
number and turn it the white side up. The puck stays on this point until the shooter either makes his
point or until he sevens out. When this happens the puck is moved to the don't come bar 12 area
and turned black side up. The significance of this device is only in tracking the game. White side
up over a point indicates the game is in progress and that this box number is the point. Black side
up means a new come out roll is about to take place.
As with all table games, you begin by changing your cash money into gaming chips. In
Craps you do this by throwing your money on the table and yelling "change". If the table is playing
well there will be a lot of people crowding around and a lot of noise, so make sure you yell out.
Also it is a good idea to wait and ask for change between rolls of the dice.
In Craps, winning or losing depends on a variety of different possible outcomes on any
roll of the two dice, and on which of these possibilities you bet. The two dice can produce many
different number combinations; some can be made several ways, others only one way. For
example, the number 6 can be rolled by two dice as follows: 5/1, 4/2, 3/3, 2/4 and 1/5. But the
number 2 can only be rolled one way: 1/1. Numbers such as 6, which can be rolled several
ways, don't pay as much as numbers which can be rolled only one way, unless you are betting
that the number will be rolled in a specific way, such has 3/3, known as Hardways. All winning
payoffs are, therefore, determined by the frequency in which any two-dice number combinations
can be rolled. Generally, the harder the combination is to roll, the more it will pay, and vice
versa.
Although really taking advantage of the many betting options can involve a considerable
degree of mastery, in its simplest form Craps is a game where players bet, either, that the shooter
will make winning rolls, or that he or she will not make winning rolls. Betting that the shooter will
make winning rolls is called betting "with the shooter" [ also called "betting right" J, and betting
that the shooter will not make winning rolls is called "betting against the shooter" [ also called
"betting wrong" ].
To bet with the shooter, you place your bet in an area marked "pass line", and this is
known as making a "line bet". The so-called pass line is a strip on the table layout marked by two
lines roughly two inches wide and it rims the entire table layout across from the Box Man. To bet
against the shooter, you peace your bet in an area marked "don't pass". This area is also a strip
on the table layout, and it rims the table directly above the pass line.
No matter what stage the game is in, whether on the come out roll, or in progress, you
can jump in immediately and place any bets. The only exception to this is the bet called the "pass
line bet with odds", which can be made only on the come out roll. You can, however, bet with the
shooter even while the game is in progress, by placing a pass line bet without odds. This is done
by placing your chips half-way over one of the two lines framing the pass line area.
Before the new shooter rolls the dice on his or her come out roll, there are a variety of
bets that can be made. The easiest and most common bets to make are the above-mentioned
pass line and don't pass line bet. But after a point is established by the shooter, you can then
place an additional bet behind your pass line bet. This is called "taking odds".
In most casinos you can bet up to double the amount of your pass line bet. This is called
"taking full odds". Some casinos offer up to 10-times odds, and this simply means that you can bet
up to 10 times the amount of your pass line bet once a point is established.
Betting the don't pass line is the exact opposite of betting the pass line. If you do this on
the come out roll, your don't pass bet wins if the shooter rolls any craps -- 2 or 3 [ties on 12] --
and loses automatically on any 7 and 11. Tieing on 12 simply means that there is no decision --
your don't pass bet neither wins nor loses, merely stays in limbo till a decision is reached on
subsequent rolls.
If the shooter establishes a point, your don't pass bet stays in action, but to win your bet
the shooter must roll a 7 before making his point. Therefore, a don't pass bet wins if the shooter
fails to make his point, but loses if the shooter does make the point. You can also take odds on a
don't pass bet.
A don't pass bet is not a bad bet, but I will not recommend it for the casual player since
it requires a solid grasp of odds mathematics as well as considerable game acumen. Betting with
the shooter is a far easier method to grasp in a short time, and offers many more advantages.
For the remainder of this chapter, therefore, I will confine all play and bet suggestions to the right
way bets.
Once the shooter establishes a point, a whole range of betting options open up in
addition to all the bets available on the come out roll.
BETTING:
BETTING THE PASS LINE (With the Dice):
When the "shooter" rolls a 7 or 11 on the first throw (The come-out roll) it is a "natural" and you
win. On the other hand, if 2, 3 or 12 rolls, it is "craps," and you lose. Any other number 4, 5, 6, 8,
9, or 10 becomes your "point." You win if the "point" repeats before a 7 rolls, and you lose if 7
shows before you make your "point." Place these bets in the area marked "Pass Line" on the layout.
BETTING THE DON'T PASS LINE (Against the Dice):
This is the reverse of betting the "Pass Line." You lose on a "natural" 7 or 11, and win if a 2 or 3
rolls. 12 is a "standoff," no one wins. If 4, 5, 6, 8, 9, or 10 rolls it becomes your "point" and you
win if 7 rolls before your "point" is repeated. You lose if your "point" is made before a 7 rolls.
Place these bets in the area marked "Don't Pass Line" on the layout.
COME BETS:
The simplest explanation of "Come" bets is that you're betting with the dice, exactly as on the "Pass
Line," except that "Come" bets are made ant time after the "come-out" roll. You win on "naturals" 7
or 11, and you lose on "craps" 2, 3 or 12. Any other number becomes the "come-point" and you
win if your "come-point" is made before a 7 rolls. You make these bets in the area marked
"Come" on the layout.
DON'T COME BETS:
The reverse of betting the "Come." You lose on a 7 or 11, and win on a 2 or 3. 12 is a
"stand-off." Here you win if 7 rolls before your "come-point" is repeated, and lose if the
"come-point" is made before a 7 is rolled. Place these bets in the area marked "Don't Come" on the
layout.
PROPOSITION BETS:
These are all one-roll bets that are decided on each roll of the dice. Any Seven pays 4 to 1...Any
Craps (2, 3 & 12) pays: 30 to 1 if the number rolled is 2 or 12 and pays 15 to 1 if the number
rolled is 3 or 11 ..... Horn bet: (a 4 unit bet wagered on 2, 3, 11 and 12) pays: 3 times your bet if
the number rolled is 3 or 11 and 7 times your bet if the number rolled is 2 or 12..... Horn-high
bet: same as the horn bet with an additional amout bet on 2, 3, 11 or 12 as you designate. These
bets are placed for you by the dealer.
HARDWAYS:
There are four possible hardway bets. "Hardway Four" (Two 2's) and "Hardway Ten" (Two 5's)
which pay 7 to 1, and "Hardway Six" (Two 3's) and "Hardway Eight" (Two 4's) which pay 9 to 1. If
any other combination of the number or a 7 is rolled you lose. These bets are placed for you by
the dealer.
BETTING THE ODDS:
You may take odds or lay odds in addition to your original bet (flat bet). The odds bet wins if your
flat bet wins and loses if your flat bet loses. The odds on 4 and 10 are two to one, on 5 and 9 the
odds are three to two, and on 6 and 8 the odds are six to five.
PLACE BETS:
You may make a "Place Bet" any time on any or all of the following numbers: 4, 5, 6, 8, 9, or 10.
If the number you have "placed" rolls before a 7 you win and are paid nine for five on the 4 and
10, seven for five on the 5 and 9, and seven for six placed on the 6 and 8.
BUY AND LAY BETS:
Pay true dice odds and may be made any time on any or all of the following numbers: 4, 5, 6, 8,
9 or 10. A buy bet wins if the number rolls before a 7. A lay bet wins when 7 rolls before the
number. 5% is charged on a buy bet and on the amount that could be won on a lay bet.
FIELD BET:
This is a one roll bet that may be made on any roll. If 3, 4, 9, 10, or 11 rolls, you win even
money. If 2 or 12 rolls you win 2 to 1. If any other number rolls you lose. This bet is placed in the
area marked "Field" on the layout.
Below is a chart that displays the possible odds of making a particular number:

*********************************************************************************************************************
Now decide which of the ways youu want to play a virtual game of Craps. Look at the Irony Games Dice Server <http://www.servtech.com/public/irony/mailroll.html>. It is the simplest approach to use and will allow you to ask questions of your instructor if you don't understand rules or betting. You'll have to exit the server after you roll, and use the email or chat features of FirstClass to question your instructor. The only problem with using this approach is that you have to figure out your winnings and losses. If trying to figure our your own winnings or losses is too much trouble, you can play a simplified version of the game at Craps + Applet = Crapplet by Steve Weiss <http://server.Berkeley.EDU/~stew/craps.html> though your betting strategies will be restricted. If you want to take more time and a little more trouble you can try a virtual Craps game at <http://www.dorcino.com/casino-home.html> a free virtual casino. Both of these sites tell you how much you won or lost on each bet and keep track of you overall winnings or losses. You might even want to play the game with a friend using real dice and poker chips as your money (make white $10, red $25 and blue $50)..
If you use the Irony Dice server, you will see the following form on your screen.
*********************************************************************************************************************
Irony Games' Dice Server
E-Mail version with PGP authentication; millions and millions of sides served!
(A version for Web-only rolls is here.)
Describe this roll:
How many dice would you like to roll? {select 2}
How many sides are on each die? {select 6}
Should anything be added or subtracted from the total roll? {select no}
You can drop either the highest or lowest die roll (or both.)
__ Drop the highest roll. {make sure these are not }
__ Drop the lowest roll.
The entire roll can be repeated; how many times? {select 1}
Mailing Information:
The subject of the mail note:
Say what this roll is for: {type in CRAPS Turn 1 roll 1 - I bet $_______ on________}
Enter this correctly or your roll will get lost!
Type in your e-mail address: {type in your email address@}
Optional:
Also e-mail the results to: {type in kempr@uslink.net}
To roll the dice, press: ROLL THEM BONES {press this button}
To reset the form, press this button: RESET
*********************************************************************************************************************
Fill it in as suggested and keep rolling dice until you've completed five turns for Scenario One and five
turns for Scenario Two. You won't need to change the form until you win or lose a turn. Then simply
change the Describe this roll section of the form. As you complete each turn make note of how much
you won or lost and explain why you bet as you did. Obviously you can use different betting strategies
for each of the scenarios.
Which ever way you choose to play your games write a one screen explanation of why you bet as you did. Make sure you explain the differences between the way you bet in scenarios one and two.
*********************************************************************************************************************
{Ideally students will submit this response using a form window and will only be permitted to continue the lesson after a sufficient number of characters have been entered.}
**********************************************************************************************************************
Most of you will use quite different strategies in the two situations. If you think back to Shirley's trips to
the cities, you'll remember she made different decisions depending on how much was at stake
(shopping versus a new job) and how likely she was to be trapped in a storm. What she was doing was
running a risk in order to achieve some gain.
Perhaps we should spend a moment thinking more carefully about the concept of risk. Not only will it
help us analyze how Shirley should bet if baby really needs a new pair of shoes; it will also help us
understand that gambling with our lives is the way of life for a creature blessed or cursed with a sense of
the difference between what is and what might be. Nicholas Rescher in his book, Risk: A
Philosophical Introduction to the Theory of Risk Evaluation and Management, indicates that the study of
"risk is part of a wider study of rationality in choice and action, part of the domain of practical
reasoning, whose object is the rational choice of courses of conduct." Risk, in this sense, is the
"chancing of ... some harm or loss; it involves knowingly acting in a way that creates or enhances
the chances of something unwanted happening. Risk exists when things may go wrong, whenever we
act and there are probabilistically indeterminate outcomes some of which are negative, like:
Possible
Negative
Action Outcome
eating indigestion
driving collision
flying crash
gambling losing
trusting Betrayal
While the notion of negative outcomes is clear enough, we may need to take a moment to understand,
probabilistically indeterminate. If you think back to Shirley's drive to the cities in the face of a pending
blizzard you have an excellent example of probabilistic indeterminacy. Every trip Shirley makes when
there is a 50% chance of a severe storm is equally likely to leave her stranded and potentially in serious
danger; but it is just as likely that she will make the trip without encountering a blizzard. Before she acts
by either going or not going, she cannot be certain of the outcome. She has no way of determining the
outcome. All she has is an estimate of how probable an event is. In the face of the uncertainty and
indeterminacy, she must guess about what to do, about how to act, about what choice she should
make. It is in acting and choosing that we take risks. As Rescher points out, we cannot eliminate risk
from living.
We are vulnerable creatures, living our lives within a sea of risks that surrounds us on every
side. The very environment we inhabit confronts us with major risks and so does virtually every
action-choice we make. From the very moment we gain a foothold on life, we have something to
lose. The question in human action is never the indefinite one of whether to accept a risk or not
-- the answer here is a foregone conclusion. The question can only be whether to accept this
risk or that one. Action is always a matter of balancing one risk off against another, of chancing
one hazard or another. (p. 9)
We do need to be careful to understand that we define acting inclusively enough, however. If Shirley is
unsure about what she should do given the possibility of the blizzard, and waits for the morning weather
forecast, or turns on her computer and calls up the local radar map, she is acting, choosing to get more
information, before making another decision. In fact, she is doing research. Many of us do the same
thing before we make major investments or purchases, looking up the Consumer Reports review of
automobiles or washing machines, comparing the interest rates we'll pay using various credit cards or
lending agencies. We'll return to research in a minute, because it turns out that learning, and thereby
reducing our uncertainty, is one of the best ways of reducing risks.
But before we do that, we need to think about two things. The first is chance itself. We live in a world
where chance operates continuously. In such a world, according to Rescher, even an all knowing actor,
one who knows all that can be known, would have to evaluate risks. He says, "In particular, if man is a
free agent whose actions are inherently unpredictable by others, then God "took a chance" in bringing
such a being to realization." His point is that fate, luck, chance, circumstance affects us one and all.
We cannot control or predict exactly what will happen in our lives. As the thinkers of the Italian
Renaissance said we must practice virtu, try to proceed with reason and skill, but we cannot control
fortuna, fortune or fate. In the end we must act in the face of uncertainty about outcomes.
What mathematical reasoning about our choices or acts does is maximize our chances of doing well,
either in terms of minimizing our losses, maximizing our gains, or, trying to have our cake and eat it to,
by minimizing loss while maximizing gain. In fact, the branch of applied mathematics called statistics
uses the nature of chance itself to discover patterns that enables us to evaluate the probability that the
judgments we make about alternatives are justified by the data we have collected about outcomes. We
will do a little reasoning of this sort shortly.
The second matter we need to think about is that sometimes, even when we can't really guess exactly
how likely some catastrophe we might face is, and we can guess that it is not very likely, we still may
make a reasonable choice to act as though the catastrophe was likely. In fact, sometimes, the worst
mistakes people make are those that ignore the possibility that seems least likely. Here analyzing risks
teaches us valuable lessons. Recently some public officials complained vigorously because, though the
Corps of Engineers and the National Weather Service warned that there was high potential for flooding
and advised citizens living in the flood plain of the Red River of the north to take out flood insurance,
they predicted a flood stage that was below the level of flooding that actually occurred. Many people did
not take out flood insurance because they though the prediction about how high the river would get was
a guarantee instead of a guess.
Visit the Pioneer Planet <http://www.pioneerplanet.com/archive/flud/dox/oth518a.htm> Web Site and
read the news feature that appeared in the Sunday, May 18, 1997 issue of The St. Paul Pioneer Press.
The article ends by quoting the mayor of East Grand Forks who wants better predictions. Most
assuredly the Weather Service and The Corps of Engineers, will use a different model, a different
pattern, as they try to guess about flooding in the Red River valley in the Future. But if their is even a
small difference between then and now, they may still be off, because flooding and weather involve
complex natural systems that exhibit sensitive dependence, that are chaotic. But we're getting ahead of
ourselves again.
What do you think the Red River valley residents should have done. Where did they make their mistake. Write a one screen or less explanation of what was wrong with their reasoning
*********************************************************************************************************************
{Ideally students will submit this response using a form window and will only be permitted to continue the lesson after a sufficient number of characters have been entered.}
**********************************************************************************************************************
Would the following analysis help you to decide what to do if you were in such a situation. Assume you
lived in the Fargo area and you had a property worth $250,000. Assume that you heard the National
Weather Service advising you in February to buy insurance. The usual way that risk analysis is
diagramed is something like the following where P= the probability of a flood exceeding predicted high
water levels.
WHY BUY FLOOD INSURANCE
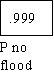

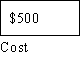

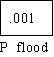

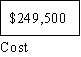
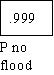

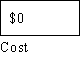



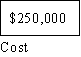
What is clear from a quick look at the diagram is that given the catastrophic nature of the potential loss,
the insurance is a small price to pay for a great deal of security. In fact as Rescher points out insurance
"provides a means of by which one hazard (losing $250,000 dollars) can be replaced by another, less
threatening one (paying $500 for insurance I don't use). What makes the decision reasonable is the
magnitude of the loss justifies the expenditure, even though the probability of the event is small. Risk
analysis can calculate the actual values of the risks involved in each course of action. If this is done in
such a case the rational choice is to run the risk of losing $500 to avoid losing $250,000. The obvious
rule is avoid being penny-wise and dollar-foolish.
Most situations where we have to make choices are nowhere near as clear cut. "Living in a sea of risk,"
both because we know what might be, could be the worst, and because we don't know enough to be
sure about what will be, we try to discover strategies for acting, for making choices about what to do. To
paraphrase Aristotle we don't worry about what is certain; we worry only about what is probable. All of
science worries precisely about what is probable. The mathematics it uses to assess probability is
statistics and at the center of statistics is the pattern of chance, of randomness, the normal distribution.
If things are randomly distributed, if they occur by chance, then we can guess about how an event will
turn out by using the characteristics of a mathematical pattern or model to make our prediction. For our
purposes we can use a simple event to illustrate how more complex predictions operate.
Consider both Shirley's trip and her betting. In each of those situations we used some patterns to help
us answer questions about what Shirley should do. Let's look at them again.
The Binomial Pattern - Trips Without Blizzard
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1

Both of these patterns can be approximated by the normal curve. For a more complete mathematical
explanation of the case involving Shirley's 50% chance of running into a blizzard you can visit
<http://frey.newcastle.edu.au/Stats/surfstat/3-2-8.html#ref:normalApproximation> SurfStat again. The
discussion there demonstrates that the binomial distribution can be approximated by the normal
distribution, especially s the number of cases grow larger.
For the moment let's ignore the froumlas and the calculations used to prove that the normal
distribution approximates the binomial distribution, and simply look at the patterns.

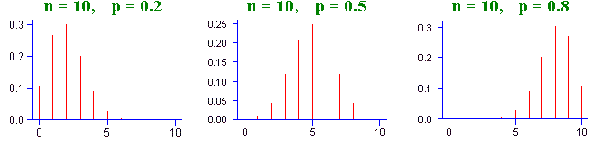
And this is a Normal Probability Distribution approximating all these distributions.

Again ignore the formulas and calculations and look at the shape. The basis for claiming that the
normal distribution can approximate the other distributions is reveled by shape, by pattern.
For throwing dice we can demonstrate the same effect for ourselves. We can, however, use virtual dice.
<http://www.mste.uiuc.edu/activity/webdice.html>
At the WebDice site you can roll a pair of dice many times with one throw. Fill out the Web Dice form
like this the first time you roll.
*********************************************************************************************************************
Welcome to WebDice!
This page will simulate the rolling of a set of dice. Use the pull-down menus to set the
parameters for the trial.
Note:This page requires a forms-compatible browser
Please choose the parameters for this trial:
Number of Sides on each die: 6
Number of Dice: 2
Number of Rolls: 10
View Sum of Dice for Each Roll?: Yes
![]()
![]()
Response times vary. However, the results usually appear somewhere between 10 and 30 seconds after submission.
*********************************************************************************************************************
Then click the Roll Dice. After a relatively short time your screen will look something like this.
**********************************************************************************************************************
WebDice Results
Here are the results of rolling 2 6-sided dice 10 times.
4 3 = 7
2 4 = 6
6 2 = 8
4 6 = 10
1 3 = 4
4 1 = 5
1 2 = 3
6 1 = 7
4 5 = 9
5 4 = 9
SUM OF ALL ROLLS = 68
Number of 1s: 4
Number of 2s: 3
Number of 3s: 2
Number of 4s: 6
Number of 5s: 2
Number of 6s: 3
4
3
2
6
2
3
********************************************************************************************************************
Arrange you scores in a distribution like this:
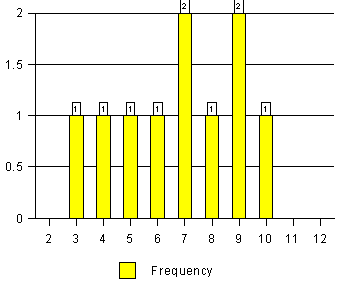
Now let's use some calculation and a formula to determine what the average score for our ten rolls was.
To do that we simply divide the total score (68) by the number of rolls we made (10).
Average score =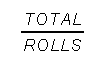 =
= = 6.8
= 6.8
.Do the same thing for 20 rolls and for 50 rolls.
Now examine the distributions and the averages and tell me in a one screen (paragraph) statement what patterns you see in your results.
**********************************************************************************************************************
{Ideally students will submit this response using a form window and will only be permitted to continue the lesson after a sufficient number of characters have been entered.}
**********************************************************************************************************************
In a measuring where the middle of a distribution is there are three ways of proceeding. The
mathematical average or mean is the one we've just calculated. Let's look for a moment at the other
two widely used measures.
The mode of a distribution is the most frequently occurring score. In this case, we have two such
scores, 7 and 9. This distribution is, therefore, bimodal. In a normal distribution the mode and the
mean are the same and the distribution is therefore unimodal.
The median if a distribution is the score above which and below which 50% of all the scores lie. In our
case that score is 7. In a normal distribution the median is the same as the mean and the mode.
Given this set of relationships we have another way of evaluating how like the normal distribution our
distributions of dice rolls are. If the mode, the mean and the median keep getting closer to one
another, our distributions are beginning to resemble the normal distribution more closely.
Let's make one more observation and computation and we will have a real sense of the power of the
pattern we've discovered. Looking at your three distributions of dice rolls, you can see that not only
does the average get closer to seven as you roll the dice more times, but the distribution of scores
around seven gets more symmetrical, more like the normal distribution. Our calculation will gives us a
measure of how scores are distributed in relation to our measure of central tendency, the average or
mean.
The way we do this is to subtract our average or mean score for all other scores.
Score Deviation Score Deviation
4 3 = 7 - 6.8 = - .2 4 1 = 5 - 6.8 = -1.8
2 4 = 6 - 6.8 = - .8 1 2 = 3 - 6.8 = -3.8
6 2 = 8 - 6.8 = +1.2 6 1 = 7 - 6.8 = - .2
4 6 = 10 - 6.8 = +3.2 4 5 = 9 - 6.8 = +2.2
1 3 = 4 - 6.8 = -2.8 5 4 = 9 - 6.8 = +2.2
Now I have to solve a simple mathematical problem. If I add this set of deviations as they stand, they will add to near zero because the positive deviations will cancel the negative deviations. But this doesn't really measure how far away from the mean all the scores are on average. We can solve the problem by ignoring the signs (±) of the numbers and adding up the deviations,
or we can
square each of the deviations , add up the squared deviations, and take the square root of the
total squared deviations.
We will use the second method which is preferred for reasons we won't go into here. Our deviations are:
Squared
Deviation Deviation
- .2 .40
+ .8 .64
+1.2 1.44
+3.2 10.24
- 2.8 7.84
- 1.8 3.24
- 3.8 14.44
- .2 .40
+2.2 4.84
+2.2 4.84
Total .8 48.32
![]() Average deviation =
Average deviation = =
=  = .695
= .695
In a standard normal distribution the mean is 0 and the average deviation is 1. For a normal
distribution ten scores with mean of seven to be a normal distribution its deviation would have to be
.700. In other words, the normal distribution approximates the distribution of our dice rolls
Now do the same calculations for your sample of dice rolls and submit your calculations using the following form:
**********************************************************************************************************************
{Ideally students will submit this response using a form window and will only be permitted to continue the lesson after a sufficient number of characters have been entered.}
**********************************************************************************************************************
Looking for patterns like the normal distribution in nature is what research, weather predicting, living and
dying is about. It turns out that the normal distribution is an excellent model for all randomly distributed
variables ranging from shoe size to intelligence and height of mountains. It is a pattern inherent in a
world governed by chance. In fact one of the standard ways scientist evaluate the results of their
research is to use the standard normal distribution to evaluate the probabilities of making errors in
reaching conclusions based on the data they have gathered. The approach they use ties together our
discussion of risk and pattern. The risks the scientists are concerned with are the risk of making
incorrect conclusions. They are concerned with two basic kinds of errors. The first, which is
conventionally called designated (alpha ) error, is the error we make when we wrongly conclude that a
factor we introduced in the experiment caused a result when, in fact, it didn't. The second kind of error,
(beta) error, is the error we make when we wrongly conclude that a factor had no effect when, in fact, it
did have an effect. Scientists want to be very careful, in many cases, to avoid risk. They want to be
as certain as they can that there conclusion is not a result of random factors. By observing a distribution
of appropriate measurements made after the "treatment" in the experiment has occurred, computing the
mean and average standard deviation and comparing their results with standard normal
distribution, they can make a judgement that the risks of making an error are 5 in 10, 1 in 100, 5 in
1000. That is they estimate the probability of error as .05, .01 or .005 respectively. In fact they can read
from the table and might conclude for, example, the probability of error in a particular case is .125. So
what, you might say, until you consider risk. If you consider risk, then it is easy to understand, that in
some cases, like those in which we're trying to evaluate the effectiveness of potentially deadly
medications in treating life threatening disease, we'd want to be very careful that a treatment didn't kill
the patient while trying to cure her. On the other hand, if the threat of death is imminent, we might risk
the potentially lethal side effects, to save the patient, a desperate last chance kind of treatment.
RISKS OF USING LETHAL DRUG TO TREAT LETHAL ILLNESS


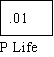

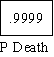




Using the drug though the probability of saving a life is small is worth the risk because it improves the
patients chances from 1 in 10000 to 100 in 10000. The way scientists arrive at the probability values in
the table is by experimenting with the treatment in question.
This business of trying to predict what will happen if is very old for the species. Not unlike soothsayers,
prophets, witch doctors of old reading everything from rabbit entrails to the stars, to give advice to the
tribe, modern scientists seek to give us the information we need to make rational choices in the face of
an uncertain future. The species was born looking for pattern in events that will enable it to choose
wisely, reducing risk, improving our chances of living better, longer; helping us decide what the true
situation is. The history of knowing is a history of finding patterns that help us explain what is, so that we
can imagine what might be and act to perfect ourselves and our world. We've learned to ask
If X, then what,
and learned by experience and experiment
If X, then Y.
In doing so the species has, over time, learned to see patterns where none were initially apparent, to
predict the unpredictable, to solve the insoluble, to cure the incurable. We have a vaccines for small pox
and polio, are on the edge of cures for cancer and aids, and are taking our first steps to the stars by
taking risks. We seek and find order in the midst of chaos by asking what if questions and
measuring probabilities.