Phys 3041 Notes
©1997 Jonathan Maps. These notes may not be redistributed or duplicated in any form, print or electronic, without permission. Permission is granted to establish electronic hypertext links to these original documents only.
We will consider here two simple circuits that make use of a resistor and capacitor in series. These two configurations will form low-pass and high-pass filters. In a filter an input voltage is applied to a circuit element (here a series R-C combination), and an output voltage is taken from some part of that circuit element. The filter will produce a modified version of the input signal, and the modifications that occur usually will depend on the frequency of the input signal. For our simple filters here, the output voltage is smaller than the input, and there will be a phase difference between the input and output signals. These filters are linear circuits in that a sinusoidal input produces as a sinusoidal output.
Low Pass Filter
The low-pass filter is a simple RC series circuit, with the output voltage taken as the voltage drop across the capacitor.

The analysis of the circuit is simple. The RC combination is viewed as a voltage divider. The procedure for finding the output voltage is similar to the analysis of the resistive voltage divider, except we must now make use of the impedance of the capacitor and carry out the analysis with complex voltages and currents, remembering to take only the real part of our results when we're done. The process is simple. Find the total series impedance of the RC combination. Use this to find the current flowing through the RC series combination. Then find the (complex) output voltage
by making use of the generalization of Ohm's law, V = IZ. In most situations like this, it is often easier to caclulate the ratio of the output voltage to input voltage
Vout(t)/Vin(t), which we will call the gain. (In fact, for these filters the gain is less than 1, so that properly speaking the signal is attenuated. Since we will often encounter this sort of ratio in connection with amplifiers later, we'll still call this ratio the gain, although that word usually suggests the output is bigger than the input.) This ratio will be complex, reflecting both a change in the the signal's amplitude and phase at the output. The magnitude of the ratio is also referred to as the frequency response of the filter, since it is usually a function of the frequency of the signal.
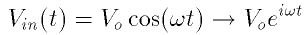

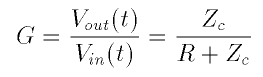
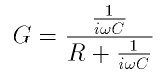
The gain G can be written in a more useful form but converting into an exponential format. Multiply numerator and denominator through by iwC first, and then by the complex conjugate, 1 - iwRC, of the resulting denominator.

This has the effect of making the denominator a real number and leaves the numerator in the standard cartesian form for a complex number, x + iy,
 which can be easily cast into exponential format:
which can be easily cast into exponential format:
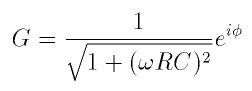
where the phase is given by
 .
.
The output voltage is then readily calculated from this gain and the input voltage:
 .
.
The final result is found by remembering to take the real part of the complex output voltage:
 .
.
This reveals two aspects of importance: the amplitude of the output is reduced compared to the input and there is a phase shift present so that the output voltage lags the input. The amplitude grows smaller as the frequency is increased, the gain tends toward zero as the frequency becomes large. The phase shift is nearly zero at low frequencies, but grows to reach one-quarter cycle at very high frequencies, where the amplitude is already negligible.
The output voltage is virtually identical to the input voltage in both amplitude and phase for low frequency signals. High frequency signals are heavily attenuated and shifted in phase. Therefore the circuit is called a low pass filter: low frequency signals are largely unaffected while high frequency signals are attenuated or filtered out. This behavior is usually displayed by a plot the the magnitude of the gain (i.e. without any phase shift information) as a function of frequency, known as the frequency response.

A rough dividing line between high and low frequencies is chosen by setting the dimensionless quantity wRC equal to 1. This occurs when w = 1/RC.
The product RC carries dimensions of time and is often called the time constant of the circuit. The low frequency limiting behavior occurs for frequencies that satisfy wRC << 1. Here the gain is practically unity and the phase shift is negligible. High frequencies correspond to those that satisfy wRC >> 1 or w >> 1/RC. Here the gain is small and given approximately by 1/wRC and the phase shift appoaches a lag of 90o.
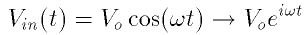

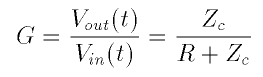
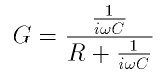

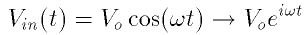

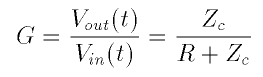
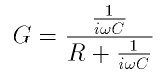


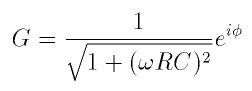
 .
. .
. .
.